Drafting the "Hat" Polykite

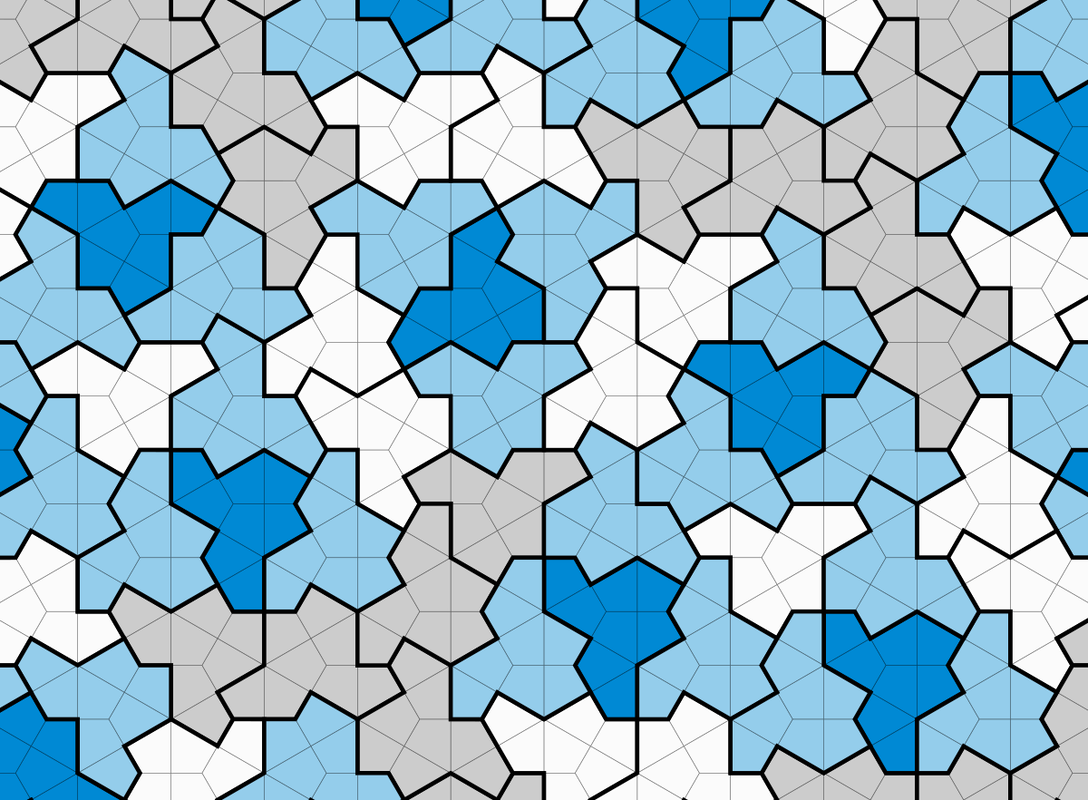
I'm not the type to jump on a bandwagon... usually.  But if that bandwagon is driven by a hobbyist mathematician and loaded with nerdy quilters from Reddit, I could make an exception.  I am pretty interested in tessellations, after all!  So today I'll introduce the "hat" einstein tile, and try to figure out how to most efficiently piece it for quilting. 

Fair warning, for those whose interest in einstein tiles is deep and mathematical... mine is not.  I'm not a fan of math; I'm a fan of the aesthetics of math!  Just as most as most of us can distinguish between fluency and awkwardness when we hear unknown languages, so most people differentiate between elegant and awkward design, without being able to explain the mathematical concepts.  For example, given several different rectangles to choose from, most people instinctively like the Golden Rectangle best, even without measuring it.  And most people are repelled by ugliness in design, without being able to tell you which mathematical law was broken! 

It is in this inchoate, instinctual way that I appreciate math.  I see something beautiful and get excited, but I don't truly understand.  I can't teach it because I don't "speak" that language.  Today's post will be laden with links to people who understand this much better than I do.  My goal is just to draw it myself, leaving the proofs to someone else! 

Tessellation Basics

A tessellation and a tiling are the same thing: any way of covering a flat surface with two dimensional shapes, so that the entire surface is covered and no pieces overlap.  A mosaic is a tiling/tesselation.  So is a pieced quilt, checkerboard, subway tile wall, and Escher doodle.  But when people hear the word "tesselation", they are usually thinking of a monotile: when the entire surface is covered with a single tile-shape, just arranged in different orientations and patterns.  A square is a monotile, as is a hexagon. 

The next concept is that of periodicity.  A square monotile has a repeat of 1, because if you lift the tiles up and move them over one row, they'll lay in the same configuration.  A hexagon has a repeat of 2.  Other tile patterns may have more distant repeats.  When a tile pattern has a repeat, it is called a "periodic" tiling.  But what if there is no repeat?  Wikipedia's article on tesselations says "a tiling that lacks a repeating pattern is called 'non-periodic'. An 'aperiodic' tiling uses a small set of tile shapes that cannot form a repeating pattern."  So the cracked ice surface pattern I have looked at before is non-periodic: you can't slide those tiles to the left right or anywhere and find a repeat.  But an aperiodic tiling would have a small number of tile shapes, arranged in ways that would not repeat.  Up until recently, the smallest example set was the Penrose tiles, discovered by Roger Penrose in the 1970's.  The tile-set contained two shapes, which were aperiodic. 

Was it possible that somewhere out there was a single shape that would tile aperiodically?  Mathematicians called this maybe-shape an "einstein tile".  (The name is all lower case, because it's German for "one stone", and is not a reference to the famous physicist.)  Since the 1970's, different tiles were introduced which were "close but no cigar" to the hoped-for einstein tile.  Some of them required a little overlap, and others had disconnected pieces, stretching the definition of tile. 

People of the Tile

David Smith of the UK is my favorite kind of geeky.  He likes art and math and diligently applying himself to the same puzzle for years.  Last November (2022), he was noodling about with tiling software, and drew a tile.  Then he tried to see how much of his computer screen he could fill with that tile before repeating a sequence.  When he'd filled his whole screen, he moved on to cardstock, and filled his table.  No repeats.  Remember what I said about the decades long hunt for an aperiodic monotile?  The jagged little shape Smith had made, based on hexagons subdivided into "kites" and re-drawn, kept on tiling without repeating, and he began to think he was on to something. 

Smith sent it to Craig Kaplan, a Canadian Computer Science Professor and artist.  The two of them called it a "Hat" because it looked like a fedora to them, and they worked on it with growing excitement.  In January, they called in reinforcements: American Chaim Goodman-Strauss, a specialist in aperiodic tilings, and British Joseph Samuel Myers, a software engineer who studies combinatorics and polyform tiling.  Together these four men did a whole bunch of math I can't begin to understand, and on March 20th 2023 (this year!), published a paper revealing the Hat monotile as truly aperiodic! 

the Hat monotile

The Hat is a polykite. Each gray shaded area is a "kite", so the tile is made of many (poly) kites.

Both these .PNG files courtesy of Christian Lawson-Perfect, who has made monotile images free in different file formats.

Image courtesy of the Cheriton School, Waterloo College, CC BY 4.0

The paper -- An aperiodic monotile, by Smith, Myers, Kaplan, & Goodman-Strauss, 2023 -- sparked enthusiasm in the normally distinct worlds of mathematicians, tiling geeks, and artists!  I learned about it on Reddit (where I lurk, because the last thing I need is an account!).  One much-crossposted headline was "New shape just dropped"... like the latest single from a band called the Geometrists!  That gave me a giggle.  On the math fora, people reacted with delight and odd dismay that it could be so simple, that it was "there all along".  Some people quibbled about the fact that the hat tile is sometimes reflected (mirrored), so is that really two tiles?  (I don't have any idea!)  I think they expected it to be an eldritch horror of a shape, instead of a bumpy fedora.  People with computers rendered it, those with laser cutters cut it, crocheters crochetted it (and did a great job!), and quilters quilted it. 

Quilters' Delight

It's the quilters, of course, who inspire me.  And, having browsed the personal websites of the paper's authors, I feel sure the quilters' spirit is closest to theirs in enthusiasm and delight for the subject.  They seem to be way more interested in playing with tiles than the grumps over at r/math, LOL!  Look at the pace of responses to the paper:

March 20, 2023 - Paper is published. 
March 21, 2023 - u/MapleNinjaMan challenges quilters of Reddit to make the hat monotile.  (That was quick!)

u/stringthing87 takes the challenge
March 23, 2023 - A Rabbit Hole Tesselated and An Update Already on the Tessellated Project (needs a name)
April 7, 2023 - How my Smith, Myers, et al Monotile quilt is Going (using 30-60-90 triangles as an EPP template)
April 16, 2023 - Block 1 of my Smith, Myers, Kaplan, and Goodman-Strauss's aperiodic monotile project
May 29, 2023 - An Update on my Aperiodic monotile project
December 4, 2023 - Aperiodic Monotile Wall Hanging is Done!!

u/Sophiedoe19 takes the challenge
March 22nd, 2023 - And so it begins! The maths grad in me couldn't turn down the Einstein tile 🤓
April 6th, 2023 - I see there is quite a group of us forming

u/silveonthelash is the first to finish! 
April 6, 2023 - Einstein tile paper piecing  Using the kite shape as the EPP template. 
April 26, 2023 - Einstein tile quilt

u/MKquilt starts later
May 25, 2023 - Einstein’s hat (t-shirts) and English Paper Piecing
​July 13, 2023 - Aperiodic monotile quilt - einstein's tshirt
July 26, 2023 - Aperiodic monotile (einstein) EPP quilt - at least I'm persistent
August 30, 2023 - Aperiodic monotile (einstein hat/t-shirt) EPP quilt
October 28th, 2023 - Finally finished!  EPP Aperiodic Monotile quilt
Finished size: 60"x80".  Cotton fabric, Tuscany wool batting.  Hand pieced.  Hand quilted with Wonderfil 12 wt.

Ann Piker (a mathematician's mom) makes him a wall hanging!
June 4, 2023 - My new Zoom background...

Lucy R on Blogger is u/KidsMathTeacher on Reddit
July 1, 2023 - My aperiodic mono-tile quilt adventure! (personal blog)
July 9, 2023  - Working on a very challenging aperiodic monotile quilt :)
August 4, 2023 - 60" square aperiodic monotile quilt top complete, whew!
Machine sewn(?).  

u/hiimmaddie's first attempt at EPP
July 6, 2023 - Starting an Einstein Tile quilt!

Diana Finkenaur (u/Finchfarmerquilts on Reddit and @finchfarmerquilts on Instagram)
August 16, 2023 - Next concurrent project ready to go! 
December 1, 2024 - Einstein tile wall hanging

Notice anything those quilters all have in common?  English Paper Piecing (EPP).  Most cut the kites from paper, wrapping and pressing fabric around the paper kites, and assembling one polykite after another, before tiling them.  This of course means multiple Y-seams, but as EPP is done by hand with small whip-stitches, it's doable.  One person (stringthing87) deconstructs the kite shape further into two right triangles, and does EPP with that.  I admire their work, it's just... I no longer have the patience for hand-sewing large projects. 

The parts of a project that excite me, as I've learned, are the problem-solving and choice-making, not just assembly.  I wonder if there's an easier way to assemble these tiles, so they can be done on the machine with straight lines.  Look at the image below, which shows the monotiling with fainter gray lines delineating the kites.  On top of that, I have annotated my own thoughts:

The right-triangles (a.k.a. 90° triangles) are the division of the polykite most useful for me, because they're the only division that allows all straight-seams.  I could assemble the rectanglular block with all straight seams, and then attach blocks to each other with all straight seams.  And if I draw the whole top, including color schemes, I could do it Foundation Paper Piecing (FPP) style.  Each rectangular block would have unique color combos and angles (i.e. there wouldn't be one single color configuration to replicate), but once assembled, the Hat shapes would emerge. 

What about the mirroring, which is present in some of the hat monotiles?  Does this translate to any of the rectangular tiles needing to be mirrored?  If you look at the blue rectangle in the image above, you'll see it's got one half-hexagon (6 right triangles) on the left, and two quarter-hexagons (3 right triangles on top and 3 on bottom) on the right.  That means it could tile in a staggered fashion, with a repeat of 2, like hexagons always do.  So I could sew one column, and then sew another with the same blocks, but shift it down a half-block, and so on.  Or, if I were determined to sew in a grid, I could mirror the blocks.  Either way would work. 

What next?

I have invited a friend to join me in doodling out a pattern for a wall-hanging!  Good company will help me not get too frustrated while fussing with rulers and angles.  I might use the design sheet from Paper Pieces as a resource, too.  Color-wise, I think this will be a good way to use up a bunch of black and white scraps (colors I don't normally use, so they pile up in my stash), with occasional pops of color. 

---

Works Cited
Department of Mathematics. (n.d.). Golden Rectangles. https://people.math.harvard.edu/~ctm/gallery/gold/index.html

Goodman-Strauss, C. (n.d.). Symmetries: Chaim Goodman-Strauss. Mathematical Imagery. http://www.ams.org/publicoutreach/math-imagery/goodman-strauss

Kaplan, C. S. (n.d.). Isohedral - The Website of Craig S. Kaplan. https://isohedral.ca/

Klarreich, E. (2023, April 4). Hobbyist finds math’s elusive “einstein” tile. Quanta Magazine. https://www.quantamagazine.org/hobbyist-finds-maths-elusive-einstein-tile-20230404/

Lawson-Perfect, C. (2023, May 31). Smith, Myers, Kaplan and Goodman-Strauss’s aperiodic monotile, in a variety of formats. GitHub. https://github.com/christianp/aperiodic-monotile

Myers, J. (2023, May 27). Polyform tiling. https://www.polyomino.org.uk/mathematics/polyform-tiling/

Smith, D., Myers, J. S., Kaplan, C. S., & Goodman-Strauss, C. (2023). An aperiodic monotile. arXiv preprint arXiv:2303.10798.  https://arxiv.org/abs/2303.10798

Smith, D. (n.d.). [Personal Website]. The Orangery. https://the-orangery.weebly.com/
This website doesn't use David Smith's name anywhere, except in a linked PDF about Melee Pairings! I only know it's his website because it was linked in articles about him, and "orangery" is part of his email address in the math paper he published.

Weisstein, E. W. (n.d.). Penrose tiles. MathWorld -- A Wolfram Web Resource. https://mathworld.wolfram.com/PenroseTiles.html

Wikimedia Foundation. (2023, April 21). Tessellation. Wikipedia. https://en.wikipedia.org/wiki/Tessellation
Last edited by Seberle, 04:58, 21 April 2023‎.

---

Edited Dec. 27, 2023 to add a project link.
​And again Dec 23, 2024 to add another project link.