Tiles and Tesselations

Now that I quilt, I see quilt patterns everywhere. Like in the pebble-mosaic walkways of the Lan Su Chinese Garden in Portland, Oregon!  Incidentally, that garden is beautiful, but in the interest of isolating patterns for blogging, I took some very boring pictures of it when I visited on November 15th, this year. 

A Pretty Picture

A Boring Picture

A tessellation, or tiling, is any way of covering a flat surface entirely, with pieces that allow neither gap nor overlap.  So -- ignoring seam allowances and just looking at surface shapes -- any pieced quilt is a tessellation or tiling.  For a fun corollary between actual floor tiles and quilts, compare this rhombitrihexagonal tiling in Spain with the "Ring Cycles" Quilt (pattern sold on Etsy).  Home Depot's mosaic tile section shows many examples of tessellation. 

People tend to use the word "tiling" when each tile is shaped exactly the same, making geometric or abstract patterns.  The word "tessellation" is preferred when the tiles are complex shapes, interlock in unexpected ways, and suggest pictures.  The work of M.C. Escher is a perfect example: he tiled unusual  intersecting shapes, then colored and detailed those tiles with pictures. 

The simplest tiling is, of course, a grid.  Squares tessellate perfectly with other squares! 

This pebble mosaic is in the Lan Su Chinese Garden, Portland, Oregon.

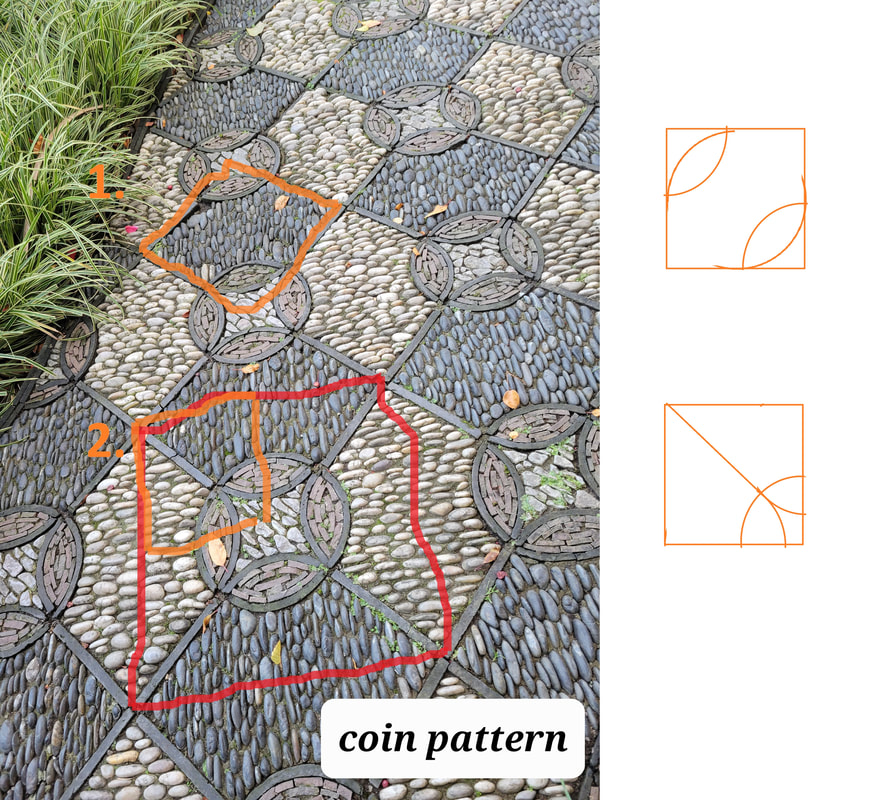
For quilting purposes, squares are a nice regular shape to aim for, since you can trim them to a uniform size to minimize the quilt top growing or shrinking during assembly.  Consider the Double Wedding Ring block I drafted; there are more complicated ways of tessellating the DWR, that involve an irregular shape and curving seams, but imagine how the slightest deviation in size or seam allowance must throw the whole quilt top off!  If I can do it with a square, why wouldn't I? 

Quilters who struggle with precision sewing sometimes choose to make their blocks a bit big from the start, knowing that they'll all end up different sizes but can be trimmed uniformly before final assembly.  I see that in eight-at-a-time HST instructions... if your quarter inch seam allowances are not regular, you're advised to start with larger squares, and trim your HSTs to size at the end.  That's also what I should have done when I had pre-made blocks someone gave me.  I should've figured out what the smallest blocks were, and trimmed them all to that size.  Naturally, the points wouldn't match (they didn't match anyway!), but the final quilt top would've been less wiggly.  Ah well, live and learn! 

In a basic grid, the tile -- the piece that repeats -- is just a blank square.  But what if there's more complexity?  The next pattern shows a basic grid overlaid with a repeating pattern.  The brain notices the swirling circles in the "foreground" first, but that's not the only way to view the pattern.  If I want to tile it, my task is to figure out what the slightly-more-complex tile is:

In step 1, I lay down the simplest shapes I see: a square, with four circles.  I pay attention to the size of the circles, and to where they intersect the edges and corners of the square.  As I draw this in MS Paint, I am merely eyeballing it, trusting my eyes to make the edge of the square tile overlap the diameter of the circle and the edge of the circle touch the corner of the square.  If I were making a paper pattern, I'd decide on the length of the radius, measure that distance from the corner along the edge of the square and so find the circle's center, and draw a circle from that center point. 

In step 2, I erase what's outside the square tile and erase two circle-lines so the other circles look like they're on top  And in step 3, I color and tile the squares, rotating them as needed to get the pattern I want. 

"But Karen," I imagine you saying, "Now those circles are bifurcated with new seamlines!  It's not the same!"  And?  So?  Therefore?  If I didn't want seams through my circles, I'd have to cut wonky-shaped pieces and assemble it in a way that doesn't allow for periodically "squaring up"... making a potentially skewed quilt. 

---

When a pattern repeats, you can delineate tiles almost anywhere.  In the next image, I draw two possible tiles; repeating either one will make the pattern happen.  If I were quilting it, I'd probably go with Tile 1, making half my tiles in a light color and half in a dark color.  Tile 2 is also doable, but more confusing because I'd need to do half with one color plan and half with the mirror-image color plan. 

Both the options I drew above assume I want a square tile, but you can easily see how the same pattern could be made with two tiles or more non-square tiles: an almond-shape in black or white, with smaller almonds in its rounded edges; and a square/diamond shape with concave sides, to fit in the center of all the mini-almonds.  (These are, of course, the technical geometrical terms for these shapes!  Or they COULD be... if people can say "squircle" with a straight face, I think I am allowed to say "mini-almonds"!)  However, for ease and uniformity of size, you can see that a regular square is still ideal if I were making a quilt. 

MISCELLANEOUS PATTERNS FOR YOU

You can play with shapes with any of the cool pebble mosaics I saw.  Some might be easy to sew just by cutting out the variety of shapes, while other might be better if simplified to a single repeating unit. 

Could be done as compound blocks with sashing?

I'd make square tiles for this one.

The tour guide told me the name of this one was the Sesame Seed.  I notice it has the same "mini-almonds" as a previous mosaic, and I wonder whether the sesame seed pattern has many variations.  Some Googling yields little information about the names of these surface designs.  I suspect there's plenty of information to be found... in Chinese! 

If you've never tried to search the internet in languages that are not your own, let me tell you: it takes luck (finding the right search term in the other language), copy-pasting, Google-translate or other translation services, and patience!  It's also hard to evaluate your sources' veracity and authority, when you're seeing everything through several filters. 

My iPhone has a marvelous function where it auto-detects the language of a website and switches it to English, with the option to toggle back and forth between the original language and the translation.  It's very helpful, but I always bear in mind that human languages have dizzying complexity and nuance, and that what I'm viewing is not as-written by the original author, nor is it even translated by a human!  This is not serious research, it's just looking. 

---

There is one more pebble mosaic I love, but it is irregular... a tiling but maybe not a tesselation?  And it, unlike the others, does merit the effort of further looking, even if that involves trying to interpret Chinese webpages.  So that one, the "cracked ice" pattern, will be a future post!